[통계적학습] 차원축소, 주성분분석 (Dimensionality Reduction, PCA) 원리 알아보기

이 포스팅은 부산대학교 통계적학습 강의를 듣고 복습차원으로 정리한 내용입니다. 박진선 교수님의 강의자료를 참고하였습니다. 

✏️ 차원축소(Dimensionality Reduction)

차원 축소에는 Feature Selection, Feature Extraction이 있다.

Feature Selection은 전진선택법, 후진선택법과 같이 전체 변수에서 특정 변수들을 선택하여 선택된 변수만 이용하여 모델을 형성하는 방법을 의미한다.

Feature extraction은 모든 변수를 이용하지만, 이 변수들을 새로운 공간에 사영시켜 사용하기 때문에 차원을 줄일 수 있다.

 

차원축소를 통해, 차원의 저주에 갇히지 않게 함으로써 예측 성능을 높힐 수 있다.

이 중, 주성분 분석(PCA)은 unsupervised 데이터 압축방법으로 Feature extraction으로 많이 쓰이는 기법이다.

오늘 포스팅은 이 주성분 분석에 대해 자세히 알아볼 것이다.

 

작년 기계학습원리를 수강하며 주성분분석에 대해 포스팅했었는데, 이번 통계적학습 강의에도 같은 내용이 나와서 반가웠다. 기계학습원리 수강할 때 배웠던 내용들이 더욱 자세해서 그 포스팅을 보며 복습했다.(아래 링크 참고)

2022.11.25 - [대학원 공부/기계학습의원리] - [머신러닝 원리] 10-2. Features

[머신러닝 원리] 10-2. Features

---

✏️ PCA(Principle Component Analysis, 주성분 분석)

주성분 분석은 위에서도 기술했다시피, Feature extraction을 위해 unsupervised로 선형 변환을 하는 작업이다.

Feature 사이의 상관관계를 기반으로 데이터의 패턴을 파악하는데 도움을 준다. 

주성분 분석의 프로세스를 간단히 말하자면 데이터의 분산이 최대화 되는 방향으로 데이터들을 projection시켜 차원을 축소하는 과정이다. 왜 분산이 최대화 되는 방향으로 데이터를 사영시키는 것일까?

내가그린그림

위 그림의 노란점이 데이터라고 했을 때, 이 노란점은 2차원 데이터라고 할 수 있다. 이 데이터를 1차원 데이터로 차원 축소시키기 위해서 특정 방향으로 사영시켜야 할 것이다. 그렇다면 A와 B중에 어떤 쪽으로 사영시켜야 가장 데이터의 정보를 가장 보존할 수 있을까? (아래 그림 참고)

A로 사영시켰을 때

B로 사영시켰을 때

내가 직접 그린 그림이라 화살표가 삐뚤삐뚤하지만, 원래는 각 A, B방향에 수직으로 떨어지는 모양이다^^,,

한눈에 봐도 B로 사영시켰을 때, A로 사영시켰을 때보다 데이터 손실이 적은 것을 알 수 있다.

이와 같이 분산이 최대화되는 방향으로 사영시켜야 2차원에서 1차원으로 차원축소했을 때,

기존 데이터의 손실을 최소화할 수 있다.

 

이렇게 분산이 최대화되는 방향을 찾았다면 그 방향과 수직(orthogonal)인 축 중에 분산이 최대화되는 축을 또 찾는다. 

이 과정을 그림으로 표현하면 아래 그림과 같다.

PC1이 첫번째 주성분이고, PC2가 두 번째 주성분이다. 

 

이러한 차원축소 과정에서 쓰이는 transform matrix를 알아보자.

먼저 차원축소 전의 feature개수가 d라면 아래처럼 표현할 수 있다. 이런 x를 feature vector라고 하며, [1*d] 형태의 행렬이다.

d개의 feature를 가진 데이터를 변형하기 위한 transformation matirx(W)는 아래와 같다. W는 [d*k]형태의 행렬이다.

위 같이, x와 W를 곱하면 z의 결과가 나오는데 z는 

차원축소되어 줄어든 k개의 feature를 가진 [1*k] 형태의 행렬이다.

 

이렇게 d차원의 데이터를 새로운 k 차원의 공간으로 변환함으로써, 제 1주성분은 가장 큰 분산을 가지게 된다.

이전의 주성분과 상관성이 없다(orthogonal-수직)는 제약 하에 가장 큰 분산을 갖는 그 다음 주성분이 생성되게 된다.

만약, 피처 간에 상관성이 있다고 하더라도, 도출되는 주성분은 서로 수직관계일 것이다. 

또한, 주성분분석은 데이터의 scale에 매우 민감하다.=> normalization이 필수적이라는 의미.

왜냐하면 V(ax)와 V(x)는 a의 제곱배만큼 차이가 나기 때문이다. 

 

✏️ PCA Process

PCA의 표면적인 과정을 정리하면 다음과 같다. 

1. 속성값들의 평균이 0가 되도록 Standardize한다.

2. 데이터를 보고 variance가 가장 큰 방향이 어느 쪽인지 찾는다. (projection시켰을 때 information loss가 가장 적은 방향)

이 방향의 선은 새로운 좌표계의 첫번째 축이다.

3. 2번에서 찾은 축에 수직인 선 중, variance가 가장 큰 선을 두 번째 축으로 설정한다.

4. 2, 3번을 차원의 수만큼 반복한 후, 각 축에 projection을 시켜보면 cumulative를 계산할 수 있는데 cumulative를 보고 끝의 몇 축을 날려버린다.(차원축소)

 

많은 사람들은 이런 표면적인 과정만 알고 있을 텐데, 이런 축을 도출하는데는 다양한 수식이 필요하다.

 

PCA의 수식적인 과정을 정리하면 다음과 같다.

1. 속성값들의 평균이 0가 되도록 Standardize한다.

2. 피처별 공분산 행렬을 만든다(d*d행렬)

3. 공분산 행렬을 eigenvectors과 eigenvalues로 분류한다.

4. eigenvalues를 내림차순으로 정렬하여, 이에 상응하는 eigenvectors를 정렬한다.

5. k번째까지의 eigenvalues에 상응하는 eigenvectors를 select.

6. 이 eigenvectors를 활용하여 위에서 언급했던 transform(projection) matrix을 만든다.

7. 이 projection matrix를 활용하여 d차원의 원래 데이터셋을 k차원의 데이터셋으로 transform 한다. 

---

이런 과정을 좀더 자세히 알아보고자 하는데, 1번은 위에서 설명했으니 패스하고

2번부터 설명하도록 하겠다.

2. 피처별 공분산 행렬을 만든다(d*d행렬)

위 수식을 보면, d차원의 데이터셋이라 d개의 feature가 존재해서 각 feature별로 분산을 구하고 그 분산을 행렬화(공분산) 한것을 나타낸다. 추후에 설명하겠지만, 1에서 평균이 0이되도록 Standardize를 했기 때문에 뮤에는 전부 0이 들어가게 된다.

 

3. 공분산 행렬을 eigenvectors과 eigenvalues로 분류한다.

기본 데이터셋을 d개의 feature와 n개의 데이터 개수를 가진 X행렬이라고 한다면, X는 (n*d) 형태의 행렬로, mean이 0로 standardized된 d개의 속성들과 n개의 데이터들로 구성되어 있다.즉 주어진 데이터를 평균이 0이 되도록 표준화 한 데이터 행렬을 의미한다.

이 X 행렬을 a방향의 unit벡터(크기가 1인 벡터)에 projection한다. 이 a벡터는 d X 1행렬이다. 이때, 특정 방향 벡터(a)는 아직 어떤 방향이 분산이 최대화되는 방향인지 모르기 때문에 임의의 방향이다. projection한다는 말은 내적을 한다는 말이랑 같기 때문에 다음과 같이 표현할 수 있다.

X의 한 행씩 a와 내적을 한다.

그 결과 Xa라는 행렬을 얻을 수 있다. 이 행렬은 n X 1 행렬이 된다. (한 행씩 n번 내적한 결과가 나오기 때문)

그리고 당연히 이 행렬값들도 평균이 0이게 된다.

 

우리는 이 Xa의 분산이 최대가 되는 a의 방향을 구해야 한다. 

Xa의 분산은 아래의 식과 같다.  

아래 식의 유도는 다음과 같다.

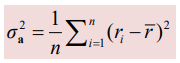
말했다시피 행렬값의 평균이 0이기 때문에 위 식에서 평균값에 0이 대입되고, 결과적으로 r제곱의 합으로 분산식을 도출할 수 있게 된다.

(n을 나누지 않는 이유는 크기 비교로만 사용되기 때문이고, r제곱의 합으로만 크기를 비교한다.)

또한, 아래 그림은  XT*X가 공분산과 같다는 것을 의미한다. (평균이 0이기 때문)

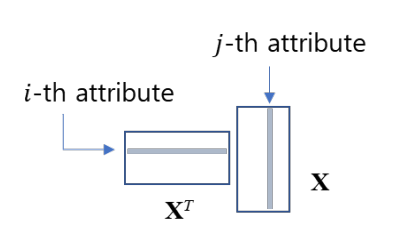
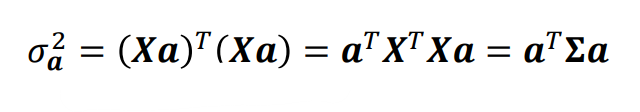
a의 크기가 Xa의 분산에 영향을 미치지 않도록 하기 위해,

위와 같은 제약조건이 있어야한다. (오직 a의 방향만 중요)

 

이런 제약조건을 완전히 만족하기 어렵기 때문에, 최대한 제약조건을 따르면서 Xa의 분산을 최대화 할 수 있는 a의 방향을 찾기 위하여 아래와 같은 식을 도출할 수 있다.

두 번째 항에서 제약조건을 지키지 못하면 패널티를 받도록 설정하는 것이다.

(이를, Lagrange multiplier라고 한다.)

이 식을 미분하기 위해 아래 표의 원리가 쓰인다.

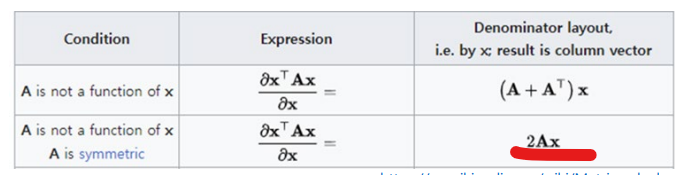
따라서 아래와 같은 식이 도출된다.

분산이 최대화 하는 값을 찾기 위해 위 미분식이 0이되는 a값을 찾아야 한다.

아래 식을 계산해주면 된다.

a가 0인 경우를 제외하고 위 식이 0이 되기 위해서는

공분산의 eigen value(람다)를 구해야 한다. 이때 a는 그에 상응하는 eigen vector가 되는 것이다. 

 

4. eigenvalues를 내림차순으로 정렬하여, 이에 상응하는 eigenvectors를 정렬한다.

5. k번째까지의 eigenvalues에 상응하는 eigenvectors를 select.

기존 데이터의 차원의 개수만큼 eigen vector, eigen value가 존재한다. 여기서, 크기 순으로 k개의 eigen value와 그에 상응하는 eigen vector를 이용하여 차원축소를 진행하게 되는 것이다.

시그마*a는 람다*a와 같기 때문에 람다가 Xa의 분산이 되는 것이다. 

즉 람다의 크기 순서대로 a의 방향이 도출되게 되고 이것이 주성분이 되는 것이다. 

 

6. 이 eigenvectors를 활용하여 위에서 언급했던 transform(projection) matrix을 만든다.

이렇게 구한 k개의 eigenvector들을 활용하여 transform matrix를 만들면 다음 수식과 같다.

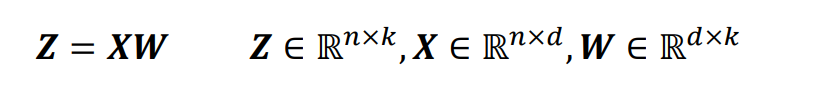
위에서도 언급했다시피, 기존 데이터셋 X(n*d행렬)에 transform matrix인 W(d*k)행렬을 곱하여 Z라는 k차원의 데이터셋을 도출해낼 수 있었다. eigen vector는 d 차원이기 때문에 이를 k개만큼 결합하면 d*k형태가 되는 것이다. 

 

차원의 수만큼 도출된 람다값을 내림차순으로 정렬한 뒤, proportion of variance 를 구할 수 있다.

그 결과를 아래와 같이 그래프로 나타낼 수 있다.

보통 95%나 99%이상일 때 까지의 축을 선택하고 나머지는 버리는 방식으로 차원축소를 진행한다.