[통계적학습] 비선형 방법 (Polynomial Regression, Smoothing Splines) 이해하기

현실의 대부분의 데이터는 비선형의 형태를 띤다. 하지만 많은 선형 모델은 이 데이터의 선형성을 가정하게 된다.

선형을 가정하기 어려운 데이터에서는 어떤 방법을 사용하면 될까?

모델의 해석력과 성능은 잃지 않으며, 선형 가정을 완화하는 방법에 대해 공부해보자.

---

 Summary

• Polynomial Regression: 차원을 증가시켜 비선형의 회귀모형을 만드는 방법
• Step Function: K개의 구간을 나눠, 각 구간별로 indicator function을 형성하는 방법 
• Regression Spline: K개의 구간을 나눠, 각 구간별로 비선형 회귀모형을 만들고 knots(경계)에서 각 모형이 부드럽게 이어질 수 있도록 제약조건을 주는 것
• Smoothing Spline: 모델의 정확도와 적당한 smooth를 고려하여 모델을 적합하는 방법
• Local Regression: K개의 구간을 나눠, 각 구간별로 선형 회귀모형을 만드는 방법

---

Polynomial Regression

기본 선형 회귀모형 식에서 다항식을 추가하면 비선형이 된다. 아래 식처럼 다항식의 차수(d)가 증가할 때마다 차원이 커지게 된다. 

 

위 다항식에서 4차원의 비선형 회귀모형은 아래 그림과 같은 모양을 띤다.

왼쪽은 나이에 따른 임금의 분포 데이터를 4차 Polynomial 모형에 least square로 적합시킨 모형이다. 점선은 95% 신뢰구간 추정치를 나타낸 것이다.

오른쪽은 4차 Polynomial 모형에 로지스틱 회귀모형을 적합하여 나이에 따라 임금이 250,000불이 넘을 확률을 그래프로 나타낸 것이다. 나이가 많아질 수록 신뢰구간이 매우 넓어져 신뢰성이 떨어지는 모습을 확인할 수 있다. 데이터 수는 3000개로 적절하지만, 고임금자의 데이터는 오직 79개 뿐이라 데이터 불균형으로 인하여 높은 variance를 보이는 것이다. 적용된 로지스틱 회귀모형식은 아래와 같다.

Step Function

K개의 구간으로 나누어 각 구간별로 indicator function을 적합한다.

예를 들면, X가 c1보다 크거나 같고 c2보다 작으면 C1(X)가 1이 된다.

즉, 해당 구간에서만 적용되는 식을 만들 수 있다.

위 그림은 K를 3으로 하여 각 3개의 구간별로 속하는 데이터를 이용하여 indicator function을 적용한 결과이다. 계단 형식이여서 step function으로 이름 붙인듯 하다. 

위 그림에서 볼 수 있다시피, 오차가 굉장히 크다.

 

---

위 Polynomial Regression과 Step Function은 Basis Function에서 파생된 방법이다. 

위 식이 Basis Function인데,  x를 어떻게 변형하냐에 따라 여러 함수로 표현될 수 있다.

즉, Polynomial Regression은

이고,

Step Function은 

인 것이다.

---

Regression Spline

Step Function 처럼 구간을 나누어서 각 구간별로 비선형 모형을 만들어보자. 3차 모형을 cubic model 이라고 하는데, 이 cubic model은 다음과 같이 나타낼 수 있다.

그리고 베타제로, 베타원, 베타투, 베타쓰리는 x값에 따라 달라진다. 수식으로 표현하자면 아래와 같다.

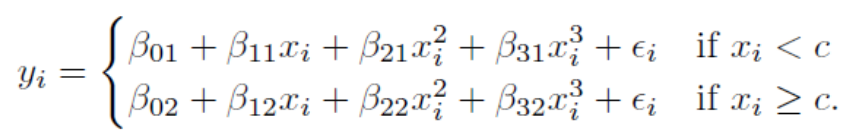
위 모형을 데이터에 적합하면 다음과 같은 형태를 보인다. 각 구간별로 주어진 데이터에 가장 잘 적합한 형태의 모형이다.

기준점(knots) 50세에서 두 모형이 이어지지 않고, 끊어지는 모습을 볼 수 있다. 연속적인 모형의 형태가 이상적이지만, 위 모형은 비연속적인 형태이다.

연속적인 모형(Spline)을 얻기 위해서 모형 적합 시, 한 가지 제약조건을 추가하면 된다.

바로 기준점 c에서 두 모형의 값이 같다는 제약조건을 주는 것이다. 이 제약조건을 주게 되면 다음과 같이 Spline 모형을 얻을 수 있다.

위 모형은 연속적이지만, 기준점에서 모형이 살짝 꺾이는 형태를 보인다. 더 부드러운 곡선의 형태를 얻기 위해 두 가지 제약조건을 더 추가한다.

두 가지 제약조건은 1차 미분이 가능하다는 것과  2차 미분이 가능하다는 것이다. 

이 제약조건들을 만족하기 위해서는

위 식(truncated power basic function) 을 base function에 추가해 준다. 여기서 제타는 기준점(knots)을 의미하는 것이다. 

cubic function이 K개의 기준점을 가지면

위와 같은데, 여기에 다음과 같이 truncated power basic function을 추가해준다.

위 식은 1차 미분, 2차 미분이 가능해진다. 직접 미분해보면 쉽게 증명할 수 있다.

이 경우, 자유도는 4∗(K+1)−3K 와 같다. 

(K+1구간마다 4개의 파라미터들이 있고 각 기준점 마다 3개의 제약조건이 붙는다는 뜻)

 

하지만, 이런 cubic spline 모형은 양 끝단으로 갈 수록  적합 데이터가 적어져서 variance가 커지는 경향이 있다.따라서 양 끝 범위에는 cubic model이 아닌 선형회귀모형을 적합시켜 모델을 안정화시킨다.이런 모델을 Natural Cubic Spline이라고 한다. 

Smoothing Spline

주어진 데이터에 얼마나 잘 적합했는지 척도인 RSS를 낮추는 것이 중요하지만 오직 이 목표로만 모델을 적합한다면 매우 과적합된 모델을 얻게될 것이다. 즉, 차원이 매우 높은 모델이 형성되어 주어진 데이터에서만 좋은 성능을 보이는 모델이 만들어지는 것이다. 그렇다면 이런 부분은 어떻게 극복할 수 있을까?

위 식을 통해 적당한 smooth를 가지며 높은 정확도를 보이는 방향으로 모델을 적합할 수 있다. 

위 식의 앞부분은 RSS이며, 해당 모델이 얼마나 주어진 데이터를 설명하지 못했는가를 나타내는 척도이다. 즉, 작을수록 주어진 데이터에 잘 적합한 것이다. 

식의 뒷부분의 람다는 smooth을 얼마나 억압할 것인가를 조정하는 파라미터이다. 모델의 이차미분식은 모델이 얼마나 smooth한가(variance가 큰가)를 의미한다. 얼마나 급격하게 변하는가를 나타내기 때문에 음수도 있을 수 있어, 제곱을 취해준다. 

람다가 0이면 주어진 모든 데이터를 만족하는 오버피팅 모델이 형성될 것이며, 람다가 무한대이면 아주 flat한 선형모델이 형성되게 된다. 

이 전체 식을 작아지는 방향으로 학습해야 우리가 원하는 목표대로 모델을 적합할 수 있다.

이러한 방식을 Smoothing Spline이라고 한다.  

Local Regression

위 식과 같이 모든 데이터에 대해 K라는 weight를 부여해서 특정 target point x0에 가까울수록 학습에 큰 영향을 미칠 수 있도록 하는 방식이다. 

위 그림에서 주황색 포인트가 target point x0이고, 연두색은 파라미터 분포이다. target point에서 멀어질수록 weight가 점점 작아지는 것을 확인할 수 있다. 이 weight를 주황색으로 표시된 동그라미 데이터를 적용하여 모델을 적합하게 된다. 이 작업을 모든 x에 대해서 실시하기 때문에 많은 용량이 소모되어 memory based model로도 불리기도 한다.