앞 포스팅 요약
앞에서 우리는 complete data가 주어졌을 때 maximize likelihood를 구했다.
데이터가 complete하다는 말은 데이터가 모든 변수에 대해 주어졌다는 의미이다.
데이터가 어떤 모델로부터 생성되었다고 가정을 하고 그 모델을 찾는 것이 task였다.
모델을 주어진 데이터로부터 추정을 했는데 고정된 structure(model)에서 parameter를 찾는 것이다.
(=베이지안 네트워크의 CPT entry들로 구성된 likelihood 식에 log를 취해서 미분한 뒤 최대가 되는 entry를 찾는다.)
이번 포스팅은 complete data가 아닌 hidden variables로 데이터가 구성된다면 어떻게 모델을 추정할지 알아보겠다.
EM 알고리즘
EM 알고리즘이란 주어진 데이터가 hidden variable로 구성되어 있을 때 유용히 활용되는 알고리즘이다.
EM알고리즘의 필요성
기본 가정은 데이터가 k개의 component distributions mixture로부터 생성되었다는 가정이다.주로 gaussian 분포의 mixture을 가정한다.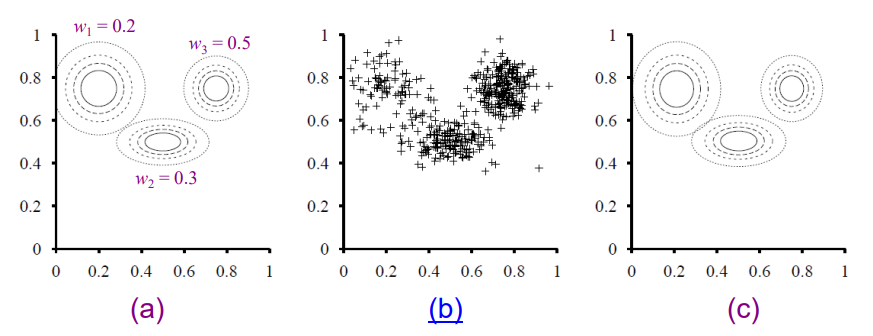
따라서 구해야하는 parameter는 w, 각 분포의 mean, covariance가 된다.
각 점을 x라 하고, i개의 각 component에서 나올 확률들의 분포를 다음과 같이 표현할 수 있다. (mixture distribution)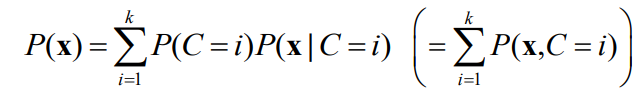
위 식은 likelihood와 같기 때문에 ML learning에 의해서 log를 붙여 미분하는 방법으로 파라미터를 구하고자 하는 것이 이전 포스팅까지의 내용이었다.
하지만, 위 식을 로그를 취하고 미분하는 작업이 결코 만만치 않다.

위 식은 completed data의 log likelihood를 구하는 작업인데 위처럼 간단하게 마무리가 되지 않기 때문이다.
그래서 다른 방안을 생각해봐야 한다.
EM 알고리즘의 원리
관점을 다르게 생각해보자
만약, 각 데이터가 어떤 component에서 나온 데이터인지 안다면 이는 completed data라고 할 수 있다.
(왜냐하면 주어진 데이터로부터 mean과 covariance를 구할 수 있기 때문)
따라서 이전 포스팅처럼 parameter를 쉽게 추정할 수 있게 될 것이다.
만약, 각 component의 parameter들을 모두 안다면 각 데이터를 해당 component로 assign(확률적으로)할 수 있기 때문에 해결 가능한 문제가 된다. 아래 식을 참고하자.

하지만 문제는
hidden variable data에서는 둘다 모른다.
EM알고리즘의 원리는 이 둘 중 하나를 아는체 하는 것이다. k-means의 원리처럼 처음에 parameter를 랜덤하게 정하고 시작하는 것이다.

만약 데이터 xi가 A, B component 중 하나에서 나온 데이터라면 A component에 속할 확률은 위와 같이 표현할 수 있다.
여기서 우리가 모르는 parameter는 A component의 평균, 분산, B component의 평균, 분산, 전체 데이터 중 A component에서 뽑힌 비율이다. (B component에서 뽑힌 비율은 1에서 빼기를 하면 되니까 포함시키지 않음)
우리는 이 파라미터들을 안다고 가정하면 우리는 위 식을 이용하여 ai 공식을 구할 수 있고
ML러닝을 통하여 아래와 같은 추정치를 얻을 수 있다.

이렇게 구해진 추정치를 이용하여 다시 ai를 reset하고 또다시 ML러닝을 반복하는 과정을 거친다.
(파라미터가 더이상 변하지 않을 때까지 )
EM 알고리즘의 procedure
위에서 설명한 원리를 정리해보겠다.
E-step
각 component의 parameter들이 주어졌다고 가정하고

위 식을 통해 j번째 데이터가 i번째 component에 속할 expected value을 계산할 수 있다. 따라서 데이터는 completed data가 된다.

pij를 구하고 그것들을 component별로 sum하게 되면 ni를 구할 수 있다.
M-step
E-step에서 completed data를 만든 후 log likelihood를 이용해 새로운 파라미터 값들을 구하는 과정을 M-step이라고 한다.

이렇게 새로 나온 파라미터들을 이용하여 다시 E-step으로 돌아가서 새로운 pij를 구하고 또다시 M-step을 하여 파라미터를 수정하는 과정을 반복한다.
EM알고리즘의 특징
EM알고리즘은 마치 gradient방식 처럼 hill-climbing하는 것과 같다.
step을 반복할수록 log-likelihood가 점점 높아지는 형태이기 때문이다.
이렇게 반복적으로 계속 parameter를 reset하게 되면 원래 우리가 추정하려던 모델보다 likelihood가 높아질 수도 있다.
보통은 local모델의 likelihood에 수렴하는 모습을 보인다.
또한 초기에 랜덤하게 parameter들을 정한 뒤 반복적으로 reset하는 방법이기 때문에 초기값에 따라 결과값이 달라질 수 있다.
따라서 이 알고리즘을 여러 번 돌려본 후 가장 좋은 것을 선택하는 것을 추천한다.
EM알고리즘을 베이지안 네트워크에 적용
위에서 설명했던 예시들을 베이지안 네트워크에 적용해볼 수 있다.
EM 알고리즘도 결국 hidden variable을 가진 베이지안 네트워크의 형식으로 해석할 수 있다.
'대학원 공부 > 기계학습의원리' 카테고리의 다른 글
| [머신러닝 원리] 12-1. 강화 학습(Reinforcement Learning) (0) | 2022.12.08 |
|---|---|
| [머신러닝 원리] 10-1. Features (0) | 2022.11.23 |
| [머신러닝 원리] 9-3. 확률적 모델(Probabilistic Models) (0) | 2022.11.17 |
| [머신러닝 원리] 9-2. 확률적 모델(Probabilistic Models) (0) | 2022.11.16 |
| [머신러닝 원리] 9-1. 확률적 모델(Probabilistic Models) (2) | 2022.11.15 |
![[머신러닝 원리] 9-4. 확률적 모델(Probabilistic Models)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fu4y9w%2FbtrRuu9GQHD%2F0MAV4cSaNKZYYm5OkYbvg1%2Fimg.png)