확률적 모델에 관해 알아보기 전에 이 확률적 모델의 기반인 베이지안 네트워크에 대해 알아보았다.
2022.11.15 - [대학원 공부/기계학습의원리] - [머신러닝 원리] 9-1. 확률적 모델(Probabilistic Models)
본격적으로 확률적 모델을 학습하기에 앞서 Statistical Learning에 대해 알아보겠다.
예시를 통해 설명해보겠다.
아래 그림에서 빨간 색 동그라미는 cherry 맛 캔디, 초록 색 동그라미는 lime 맛 캔디이다.
각 bag별로 캔디가 다르게 구성되어 있다.


하나만 설명하자면, cherry candy가 75%+lime candy가 25%로 구성 된 bag이 전체 bag 중 20%라는 의미이다.
어떠한 bag을 선택했을 때, 이 bag이 h1, h2, h3, h4, h5 중 어떤 가방일지
그 bag에서 candy를 하나씩 꺼냈을 때 그 다음 나올 candy는 어떤 맛의 candy인지의 확률을 도출할 수 있다.
이렇게 확률적으로 어떤 질의를 도출해낼 수 있는 것이 Statistical Learning인데
Bayesian learning은 이 Statistical Learning의 한 종류이다.
Bayesian learning
training data d가 d=d1, d2,...,dN라고 할때 각 hypothesis의 확률은 베이지안 룰에 의해 다음과 같이 표현할 수 있다.
(normalization constant에 관한 설명은 이전 게시물에서 확인할 수 있다.)

즉, 어떠한 candy(d)가 나왔을 때 어떤 bag(hi)에서 나왔을 확률에 대한 표현이다.
여기서 P(hi|d)는 posteriori probability, P(hi)는 prior probability, P(d|hi)는 likelihood이다.
그렇다면 어떠한 candy가 나왔을 때 그 다음 candy는 어떤 맛일 확률에 대한 분포는 어떻게 될까?
marginalization rule과 conditioning rule에 의해 다음과 같이 표현할 수 있다.

이전에도 말했듯이 굵은체 P와 일반 P와는 다른 것이다.
위 식에서 맨 오른쪽 식을 이용하여 P(X|d)를 계산하는 것을 베이지안 러닝이라고 한다.
베이지안 러닝의 특징은 가장 좋은 hypothesis를 찾을 필요가 없다는 점이다.
즉, 가장 확률이 높은 bag을 찾을 필요가 없고, 위에서도 보았듯이 각 확률을 모두 동원하여 다 더한다는 점이 특징이다.
P(hi|d)부분이 어떤 bag일 확률이므로 P(X|hi)에 곱을 해줌으로써 가중치역할을 한다는 점을 기억해야 한다.
위 식은 어떠한 가정이나 trick을 쓰지 않은 개념적으로 완벽한 수학적 공식이지만 hypothesis space가 너무 커지게 되면 계산이 부적절하다는 단점이 있다.
따라서 이 베이지안 러닝의 대안으로 MAP러닝과 ML 러닝을 제안한다.
Maximum a posteriori(MAP) learning
베이지안 러닝에서 가중치역할을 하던 P(hi|d) 중 가장 큰 h를 이용하여 learning하는 방법이다.
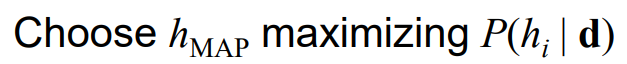
즉,

위와 같은 식으로도 표현할 수 있다.
minimize -logP(d|hi)-logP(hi)에서 description length라고 표현한 이유는
모델을 설명하는 description length를 최소화하는 의미이기 때문이다.
-logP(d|hi)는 L(D|m)으로 표현 가능하고 모델의 error를 encode하는데 필요한 bits로써, 정확도가 100%라면 이 L(D|m)은 0이다.
-logP(hi)는 L(m)으로 표현 가능하고 모델 전체를 표현하는 description length를 의미한다. 복잡하고 특이한 값이 내는 모델이라면 이 수치는 커지게 된다.
Maximum likelihood (ML) learning
P(d|hi)가 가장 큰 h를 learning 하는 방법이다.

위에도 적혀있듯이 데이터에 가장 잘 fit되는 것을 get하는 것이다.
위 MAP공식에서 P(d|hi)는 잘 맞출수록 커지게 된다. 하지만 이는 과적합의 위험이 있으므로 P(hi)를 고정한 상태로 P(d|hi)를 최대화하자는 것이 ML러닝의 의미이다.
P(hi)를 고정한 상태라는 것은 모델의 복잡도를 고정한다는 의미이므로
모델의 structure는 고정한 채로 parameter만 수정(P(d|hi)가 최대가 되도록)하는 것을 말한다.
다시 본론으로 돌아가서,확률적 모델의 주요 task는 주어진 데이터가 어떤 모델(hypothesis)에서 나왔는지를 가정하는 것이고
이를 density estimation이라 부른다.
학습된 모델의 모든 변수의 값들을 포함하고 있을 때 데이터는 complete하다고 한다.
위에서도 말했듯이 ML parameter learning은 structure은 고정되어 있고 parameter를 찾는 것이다.
종류는 두가지가 있다.
- Discrete models
- Continuous models
(파라미터 없이 학습할 수 있는 density model도 있음(nonparametric model). 나중에 따로 포스팅하겠다.)
Discrete models
위에서 들었던 candy예시는 discrete model에 해당한다.만약 우리가 N개의 candy의 껍질을 깐다고 가정하자.그리고 candy가 cherry맛일 확률을 쎄타라고 하자.

c개의 cherry맛 캔디와 l=N-c개의 lime맛 캔디가 있다.이것은 i.i.d. 관측치 이므로

이처럼 표시할 수 있다.
위 식처럼 고정된 structure에서 쎄타를 구하는 것이 이 probabilistic model의 task이다.
쎄타를 구하기 위해 아래와 같은 식으로 변형한다.

결국, 세타는 우리가 원래 알고있던데로 전체 candy 수 분의 cherry맛 candy의 개수로 쎄타를 구할 수 있었다.
(만약, c가 0이라면 Laplace correction을 사용하여 확률이 0이 되지 않게 바꿔준다.)
만약 하나의 파라미터가 아닌 multiple parameters라면?

위와 같이 파라미터가 3개인 경우에 대해 설명해보겠다.
맛이 체리맛일 확률은 세타
맛이 체리맛이고 체리맛포장으로 쌓여져있을 확률은 세타1
맛이 체리맛이고 라임맛포장으로 쌓여져있을 확률은 세타2
그렇다면 체리맛 캔디가 라임맛포장으로 쌓여져있을 likelihood는 어떻게 될까?

N개의 캔디가 있고 그 중 c개의 체리캔디 , l(=N-c)개의 라임캔디로 구성되어 있다.
rc:체리맛포장으로 쌓여진 체리캔디 개수
rl: 체리맛포장으로 쌓여진 라임캔디 개수
gc: 라임맛포장으로 쌓여진 체리캔디 개수
gl: 라임맛포장으로 쌓여진 라임캔디 개수
이 경우, 전체 캔디 데이터에 대한 likelihood의 공식은 다음과 같다.

복잡해보이지만 사실 별거 없다.
likelihood를 최대화 시키는 세타들을 구하기 위해 log를 씌우면 다음과 같아진다.

위 식을 전개하면 아래와 같이 우리가 알던 그 식이 나온다.

Continuous Models
continuous models은 위의 discrete model처럼 확률로 table을 형성할 수 없다.
따라서 확률밀도분포(linear gaussian function 등)를 이용해야한다.
discrete model에서는 model structure만 고정하였으나
continuous model에서는 structure 뿐만 아니라 확률밀도분포도 고정해야한다.
여기서 파라미터들은 평균이나 sd처럼 확률밀도분포를 변화시킬 수 있는 값들이다.
예시로, linear gaussian 모델을 들겠다.

(a)와 같은 확률밀도분포에서 (b)와 같은 데이터가 나왔다면
(b)로부터 (a)를 복원할 수 있을까?
(linear gaussian이라는 것은 알고있는 상태에서 상세 파라미터들을 유추할 수 있냐는 뜻)
(a)그래프를 보면 sd는 모두 같은 상태에서 mean만 x에 따라 선형적으로 변하는 gaussian 모델을 형상화한 것이다.
(그래서 이름이 linear gaussian)
(b)그림은 (a)에서 50개의 점들은 뽑은 것이며 x에 따른 noise에 때문에 선위에 분포하지 않고 선 주변으로 분포해 있는 것이다.
따라서,

noise를 보고 x에 따라 선형적인 mean을 찾는 것이 task라고 할 수 있다.

linear gaussian의 식은 위와 같고 시그마는 fixed 되어 있다.
여기서 중요한 점은 우리가 궁금한 것은 conditional likelihood를 최대화 하는 mean값이 궁금한 것이다.

즉, x와 y 모든 상황을 joint하여 likelihood를 구했던 discrete 모델과는 달리
x를 조건으로하여 y가 일어날 likelihood를 최대화 시키는 것이 중요 포인트이다.

log likelihood를 최대화시키기 위해 위와 같이 변형하게 되면

위 값을 최소화해야 하는 문제로 바뀌게 된다.
결과적으로 이것은 linear regression에서 sum of squared errors를 최소화 하는 문제와 같게 되는데,
이는 gaussian noise에서 sd를 고정시키고 linear fit을 ML러닝하는 것과 같은 의미이다.
(ML 러닝의 의미가 결국 얼마나 모델이 데이터와 잘 fit됐는냐였으니까)
Nonparametric Models
만약 구조자체도 없는 모델로부터 나온 데이터들은 어떻게 모델을 추정할까?

오른쪽 그림을 보면
각 점에서 가장 가까운 10개(k개)의 점들이 포함될 수 있도록 원을 그린다.
모든 점에서 원을 그리게 되며 각 점에서 가장 작은 원들을 통해 왼쪽의 그림처럼 확률밀도분포를 추정하게 된다.

k가 무엇이냐에 따라 예측되는 확률밀도분포가 달라지는 것을 확인할 수 있다.
'대학원 공부 > 기계학습의원리' 카테고리의 다른 글
| [머신러닝 원리] 12-1. 강화 학습(Reinforcement Learning) (0) | 2022.12.08 |
|---|---|
| [머신러닝 원리] 10-1. Features (0) | 2022.11.23 |
| [머신러닝 원리] 9-4. 확률적 모델(Probabilistic Models) (0) | 2022.11.17 |
| [머신러닝 원리] 9-3. 확률적 모델(Probabilistic Models) (0) | 2022.11.17 |
| [머신러닝 원리] 9-1. 확률적 모델(Probabilistic Models) (2) | 2022.11.15 |
![[머신러닝 원리] 9-2. 확률적 모델(Probabilistic Models)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbjKd2N%2FbtrRnOgQsXK%2FZOxutFYkNUQvEqjNkqbgwK%2Fimg.png)
