[머신러닝 원리] 11. 앙상블 모형(Model Ensembles)

하나의 모형으로만 학습을 하고 예측을 하게 되면, train 데이터가 살짝만 바뀌어도 모형이 쉽게 바뀌면서 예측값도 달라지게 된다.(variance가 큼)
error component에는 bias와 variance가 있는데 앙상블 기법은 variance에 대처하기 위한 방법이다.
train 데이터의 여러 version을 통해 다양한 예측 모형을 만들어서 그 결과들을 취합하는 것이다.
그렇다면 이 version은 어떻게 구성하는 것일까?
1. Reweighted: 각 train data instance마다 각자 다른 weight을 부여해서 weight가 큰 instance들의 모델이 misclassificaion을 하였을 경우 더 큰 패널티를 주는 방식
2. Resampled: train data를 여러번 샘플링하여 각기 다른 instance를 가진 train 데이터의 subset을 만들어서 모델을 학습하는 방식
이렇게 나온 결과들을 어떻게 취합할까?
1. 간단히 평균을 취하는 방법(수치속성)
2. 다수결로 결정하는 방법(모델들마다 가중치를 달리함)

이 앙상블 기법의 대표적인 방법이 배깅, 부스팅이 있는데 하나씩 살펴보자.

배깅

배깅이라는 말은 Bootstrap aggregating의 줄임말로, 샘플링을 여러번해서 나온 train데이터들의 모델 학습 결과를 취합해 결과를 내는 방법이다.
여기서 Bootstrap은 원래 주어진 train 데이터의 수만큼 train 데이터에서 복원추출하는 것이다. 즉, 데이터 크기는 같지만 같은 instance가 중복되어 존재할 수도 있고 또는 하나도 뽑히지 않는 instance가 존재할 수도 있는 샘플링 기법이다.
만약 n개의 데이터 중 한 instance가 n번의 복원 추출에서 안뽑힐 확률은 아래와 같다.

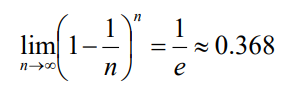
즉, 0.368의 확률로 n번 중 한번도 안 뽑힐 것이다. 생각보다 안 뽑힐 가능성이 꽤 크다.
이렇게 여러번 부트스트랩 방법으로 샘플링하게 되면 다양한 train 데이터들의 집합을 얻을 수 있다.
각 train데이터별로 모델을 학습하고 나온 결과들을 Voting 또는 averaging방법으로 취합하게 되며, 이때 각 모델의 가중치는 모두 동일하다.

만약 decision tree같이 unstable한 모델같은 경우 배깅을 통해 큰 성능상승을 기대할 수 있다.

배깅을 의사결정나무에 적용한 사례 중 가장 성능이 좋은 랜덤포레스트 모형을 잠시 소개해보겠다.
랜덤포레스트는 부트스트랩 과정에서 기존 데이터 크기만큼 샘플링하는 것이 아닌, 다른 크기로 샘플링하여 train데이터 subset을 만든다. 이는 모형의 앙상블의 다양성을 훨씬 더 증가시킨다. 또한, 기존 데이터 개수보다 적은 개수로 샘플링한뒤 의사결정나무를 만들기 때문에 시간이 비교적 적게 든다.

부스팅

배깅은 러닝 알고리즘의 불안정성을 (분산이 큼) 줄일 수 있는 상황을 이용한 방법이고, 각 모델이 독립적으로 만들어진다. 각 모델이 취합될 때 weight가 동등하게 취합된다.

이에 반해,
부스팅은 각 모델이 독립이 아님. 서로 보완하는 관계로 이루어진다. 앞서 만들어진 모델을 보고 보완하기 위한 방법으로 weight를 바꾸어서 학습하는 방법임. 앞에 모델이 잘못 분류한것에 weight를 더 줘서 학습함. (잘못 분류한 instance들을 이후 모델에서는 잘 분류할 수 있도록) 마지막에 다수결을 하는데 동등하게 취합되는 것이 아니라 confidence에 따라 가중치를 주고 취합됨(train데이터에서 error rate가 낮으면 confidence가 높아짐)

weight를 부여하는 방법에 대해 알아보자.
모델의 에러율은 0.5보다 작아야한다는 가정 하에서만 부스팅이 동작한다.
example에 각자 가중치를 부여하게 되는데, 분류가 잘못된 example의 가중치를 다 합치면 0.5가 되도록 가중치를 부여해야 한다. 처음에는 모두 동등한 weight를 가진 채로 시작한다.
instance가 100개가 있다면 각자 1/100의 weight를 가짐.
이 때는 잘못 분류된 example들의 weight 합은 error rate와 같게 된다.
100개중 30개가 error라면 error의 가중치 합은 30/100으로 error rate와 같다.
여기서 잘못 분류된 example들에 1/(2*error rate)를 곱해주어 총합이 0.5가 되도록 만든다.
모델의 에러율은 0.5보다 작다는 전제가 있기 때문에 weight가 증가할 수 있는 것이다.잘 분류된 example에는 1/(2*(1-error rate))를 곱해주어 weight가 감소할 수 있도록 한다. 나중에 voting할 때 모델 자체의 weight는 어떻게 부여할까?

위와 같은 방식으로 error rate가 크면 모델 weight가 감소하는 형태이다.

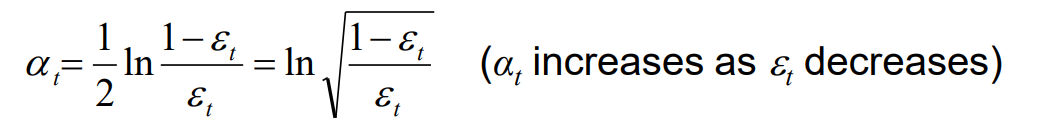
모델이 오분류하는 이유는 세가지가 있다.1. 피처들은 모두 같으나 다른 클래스로 분류되는 경우=> 모델에 쓰이지 않은 다른 피처에 의한 것일 가능성 높음2. 편향: 모델 표현력 문제로써, 표현력이 부족한 모델은(linear model) 높은 편향을 보여준다.3. 분산: boundary가 train 데이터에 너무 의존하게 되면 unstable한 모델이 되어 분산이 커지게 된다. 낮은 편향을 가진 모델들이 주로 높은 분산을 갖는 경향이 있다.


배깅이 모델의 편향을 낮추는 역할을 할수도 있지만 부스팅만큼 효과를 보지 못한다.배깅은 주로 분산을 낮추는 역할을 한다.부스팅은 편향을 낮추는 역할을 한다. 배깅은 주로 분산이 높은 모델들의 결합에 주로 사용되며 부스팅은 높은 편향을 보이는 모델들에 주로 사용된다.부스팅은 example들의 마진을 높이는 데 효과적이다. (이미 boundary에 의해 옳게 분류가 되었음에도 불구하고)또한, train 데이터에서 error가 0여도 부스팅을 진행한다면 test 데이터에서 더 좋은 성능을 가져오는 경우도 있다.